The Hairy Ball Theorem

ದಿನಾಂಕ  07 ಆಗಸ್ಟ್ 2011ರ ಸಂಚಿಕೆ...

ಬಾಚಿದ ಕೂದಲು ಮತ್ತು ಬೀಸುವ ತಂಗಾಳಿ

* ಶ್ರೀವತ್ಸ ಜೋಶಿ

[ಈ ಲೇಖನವನ್ನು ನೀವು ವಿಜಯ ಕರ್ನಾಟಕ ಇ-ಪೇಪರ್‌ನಲ್ಲಿಯೂ ಓದಬಹುದು.] * * * ಮಹಾತ್ಮ ಗಾಂಧಿಯವರ ಉಲ್ಲೇಖದಿಂದ ಇದನ್ನು ಆರಂಭಿಸಿದರೆ ನೀವು ಥಟ್ಟನೆ ಕೇಳಬಹುದು- “ಬಾಪೂಜಿ ಬೊಕ್ಕತಲೆಯವರು. ಅವರೆಲ್ಲಿ ಕೂದಲು ಬಾಚುತ್ತಾರೆ?” ಎಂದು. ನಿಮಗೆ ಆ ತರ್ಲೆ ಪ್ರಶ್ನೆಯೂ ನೆನಪಾಗಬಹುದು- ‘ಸೈಕಲ್ ಮೇಲೆ ಬಾಪೂಜಿ ಪೂರ್ವದಿಂದ ಪಶ್ಚಿಮದತ್ತ ವೇಗವಾಗಿ ಹೋಗುತ್ತಿದ್ದರೆ ಅವರ ಕೂದಲು ಯಾವ ದಿಕ್ಕಿಗೆ ಹಾರುತ್ತಿರುತ್ತದೆ?’ ಹೋಗಲಿಬಿಡಿ, ರಾಷ್ಟ್ರಪಿತನ ಬಗ್ಗೆ ತಮಾಷೆ ಸಲ್ಲ. ಬದಲಿಗೆ ಅವರ ಆತ್ಮಚರಿತ್ರೆಯಿಂದ ಒಂದು ಸಣ್ಣ ಪ್ಯಾರಗ್ರಾಫ್ ಓದೋಣ. ಇವತ್ತಿನ ಅಂಕಣಕ್ಕೆ ಸಂಬಂಧಿಸಿದ್ದೇನೋ ಅದರಲ್ಲಿ ನಮಗೆ ಸಿಗುತ್ತದೆ. “ಡಾ.ಮೆಹ್ತಾ ನನ್ನನ್ನು ನೋಡಲಿಕ್ಕೆಂದು ಲಂಡನ್‌ನ ವಿಕ್ಟೋರಿಯಾ ಹೊಟೇಲ್‌ಗೆ ಬಂದಿದ್ದರು. ಹೀಗೇ ಮಾತನಾಡುತ್ತಿರುವಾಗ ನಾನು ಅವರ ಟೋಪಿಯನ್ನು ತೆಗೆದುಕೊಂಡು ಅದೆಷ್ಟು ಮೃದುವಾಗಿದೆ ಎಂದು ಸವರಿ ನೋಡಿದೆ. ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಸವರಿದ್ದರಿಂದ ಅದರ ಉಣ್ಣೆಯೆಲ್ಲ ಎದ್ದು ನಿಂತು ಒಂದು ರೀತಿಯಲ್ಲಿ ವಿಕಾರವಾಗಿ ವಿರೂಪವಾಗಿ ಹೋಯ್ತು. ಡಾ.ಮೆಹ್ತಾ ನನ್ನನ್ನು ತಡೆಯುವಷ್ಟರಲ್ಲಿ ತಪ್ಪು ನಡೆದುಹೋಗಿತ್ತು. ಅದು ನನಗೆ ಒಂದು ರೀತಿಯ ಎಚ್ಚರಿಕೆಯೂ ಆಯಿತು...” - ಹದಿನೆಂಟರ ವಯಸ್ಸಿನಲ್ಲಿ ಬ್ಯಾರಿಸ್ಟರ್ ಓದಲಿಕ್ಕೆ ಲಂಡನ್‌ಗೆ ಹೋಗಿದ್ದ ದಿನಗಳ ಬಗ್ಗೆ ಬಾಪೂ ಬರೆದಿರುವುದರಲ್ಲಿ ಈ ಭಾಗ ಬರುತ್ತದೆ. ಅವರ ವ್ಯಕ್ತಿತ್ವದ ಕುರಿತು ಹೇಳಲಿಕ್ಕೆ ಇದನ್ನಿಲ್ಲಿ ಉಲ್ಲೇಖಿಸಿದ್ದಲ್ಲ. ಟೋಪಿಯನ್ನು ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ ಸವರಿದಾಗ ಉಣ್ಣೆ ಎಳೆಗಳು ನಿಮಿರಿ ಟೋಪಿ ವಿಕಾರವಾಗುವ ಚಿತ್ರವನ್ನು ಕಲ್ಪಿಸಿಕೊಳ್ಳಿ, ಅಷ್ಟು ಸಾಕು. ಟೋಪಿ ನಿರ್ಜೀವ ವಸ್ತು, ಹಾಗಾಗಿ ಪರವಾಗಿಲ್ಲ. ಒಂದುವೇಳೆ ನಿಮಗೆ ಬೆಕ್ಕನ್ನು ಪ್ರೀತಿಯಿಂದ ನೇವರಿಸುವ ಅಭ್ಯಾಸವಿದ್ದರೆ!? ಅಪ್ಪಿತಪ್ಪಿಯೂ ನೀವು ಬೆಕ್ಕಿನ ಬೆನ್ನನ್ನು ವಿರುದ್ಧ ದಿಕ್ಕಿನಲ್ಲಿ (ಬಾಲದಿಂದ ತಲೆಯ ಕಡೆಗೆ) ಸವರಿದ್ದೇ ಆದರೆ ಬೆಕ್ಕಿಗೆ ಅದು ಸ್ವಲ್ಪವೂ ಇಷ್ಟವಾಗುವುದಿಲ್ಲ. ಸಿಟ್ಟಿನಿಂದ ಅದು ನಿಮ್ಮನ್ನು ಪರಚಲೂಬಹುದು. ತಲೆಯಿಂದ ಬಾಲದ ಕಡೆ ನೇವರಿಸಿನೋಡಿ. ಆರಾಮಾಗಿ ಮುದ್ದು ಮಾಡಿಸಿಕೊಳ್ಳುತ್ತದೆ ಬೆಕ್ಕು. ಅಲ್ಲಿಗೆ ನಾವು ಇವತ್ತಿನ ಮುಖ್ಯ ವಿಷಯಕ್ಕೆ ಬಂದೆವು. ಇದು ಗಣಿತಶಾಸ್ತ್ರದ ಒಂದು ಪ್ರಮೇಯ. ‘ಕೂದಲಿರುವ ಚೆಂಡಿನ ಪ್ರಮೇಯ’ ಎಂದು ಇದರ ಹೆಸರು. ಇಂಗ್ಲಿಷ್‌ನಲ್ಲಾದರೆ The Hairy Ball theorem. ಇದೇನನ್ನುತ್ತೆಂದರೆ “ಟೆನ್ನಿಸ್ ಬಾಲ್ ಅಥವಾ ಬ್ಯಾಡ್ಮಿಂಟನ್ ಚೆಂಡಿನಂಥ ಕೂದಲಿರುವ ಚೆಂಡನ್ನು ಚಿಕ್ಕದೊಂದು ಬಾಚಣಿಗೆಯಿಂದ ಬಾಚಿದರೆ, ಚೆಂಡಿನ ಮೇಲ್ಮೈಯ ಅಷ್ಟೂ ಕೂದಲನ್ನು ಮಟ್ಟಸವಾಗಿ ಬಾಚುವುದು ಸಾಧ್ಯವಾಗದು. ಎಲ್ಲೋ ಒಂದುಕಡೆ ಒಂದಿಷ್ಟು ಕೂದಲು ನೇರ ನಿಲ್ಲಬೇಕಾಗುತ್ತದೆ. ಇಲ್ಲವೇ ಅಲ್ಲಿ ಪುಟ್ಟದೊಂದು ಬೈತಲೆ ಅಥವಾ ‘ಸುಳಿ’ಯಂಥ ರಚನೆ ಉಂಟಾಗುತ್ತದೆ. ಆ ಭಾಗದಲ್ಲಿ ಕೂದಲಿಲ್ಲದೆ ಚೆಂಡಿನ ಬರಿಮೈ ಕಾಣಿಸಿಕೊಳ್ಳಬೇಕಾಗುತ್ತದೆ.”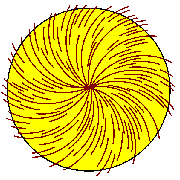 ಇದೇನಪ್ಪಾ ಈ ವಿಜ್ಞಾನಿಗಳಿಗೆ/ಗಣಿತಜ್ಞರಿಗೆ ಮಂಡೆ ಸರಿ ಇಲ್ವಾ? ಬಾಚಣಿಗೆಯಿಂದ ಮಂಡೆ ಬಾಚುವುದು ಬಿಟ್ಟು ಯಾರಾದ್ರೂ ಚೆಂಡು ಬಾಚುತ್ತ ಕೂರುತ್ತಾರಾ? ಇದೊಳ್ಳೇ ಕೆಲಸವಿಲ್ಲದ ಬಡಗಿ ಅಂಡು ಕೆತ್ತಿದ ಕಥೆಯೇ ಆಯ್ತಲ್ಲಾ? ಹಾಗೆಂದುಕೊಳ್ಳಬೇಡಿ. ಚೆಂಡು ಒಂದು ಪರಿಪೂರ್ಣ ಗೋಲಾಕಾರ. ಈ ಪ್ರಮೇಯವನ್ನು ಅರ್ಥಮಾಡಿಕೊಳ್ಳಲಿಕ್ಕೆ ಸುಲಭವಾಗಲೆಂದು ಚೆಂಡನ್ನು ಆಯ್ದುಕೊಂಡದ್ದು. ನಮ್ಮನಿಮ್ಮ ತಲೆಯನ್ನೇ ‘ಕೂದಲಿರುವ ಚೆಂಡು’ ಎಂದುಕೊಂಡರೂ ಆಗುತ್ತದೆ. ಬೋರಲಾಗಿಸಿದ ಅರ್ಧಗೋಲಾಕಾರ ನಮ್ಮ ತಲೆಬುರುಡೆ. ಅದರ ಮೇಲಿನ ಕೂದಲನ್ನು ಬಾಚುವಾಗಲೂ ಅಷ್ಟೇ, ಎಲ್ಲ ಕೂದಲನ್ನೂ ಫ್ಲಾಟ್‌ಆಗಿಸಿ ತಲೆಬುರುಡೆ ಮುಚ್ಚುವುದಕ್ಕಾಗದು. ಎಲ್ಲೋ ಒಂದಿಷ್ಟು ಕೂದಲು ಜುಟ್ಟಿನಂತೆ ನೇರ ಇರಬೇಕಾಗುತ್ತದೆ (ಕಾಮಿಕ್‌ಸರಣಿಯ ‘ಟಿನ್‌ಟಿನ್’ ನೆನಪಾದನೇ?) ಇಲ್ಲವೇ ನಮಗೆಲ್ಲರಿಗೂ ಇರುವಂತೆ ತಲೆಯಲ್ಲಿ ಒಂದು (ಕೆಲವರಿಗೆ ಎರಡು) ಸುಳಿ ಇರಬೇಕಾಗುತ್ತದೆ. ಅಲ್ಲಿ ಕೂದಲೇ ಇಲ್ಲದೆ ತಲೆಬುರುಡೆ ಕಾಣುತ್ತಿರುತ್ತದೆ. ನಿಜವಾಗಿಯೂ ಹೀಗೊಂದು ಗಣಿತ ಪ್ರಮೇಯ ಇರುವುದು ಹೌದೇ? ಏಕೆಂದರೆ ಇದರಲ್ಲಿ ಗಣಿತವೇನೂ ಗೋಚರಿಸುತ್ತಿಲ್ಲ್ಲ! ನಿಲ್ಲಿ, ಗಣಿತದ ಪದಗಳನ್ನೇ ಬಳಸಿ ಈ ಪ್ರಮೇಯವನ್ನು ಹೇಗೆ ಹೇಳಬಹುದು ನೋಡೋಣ- Given a tangential vector field on the surface of a sphere in three-dimensional space, there must be at least one point where the field is zero. ಗೋಲಾಕಾರದ ಮೇಲೆ ಸ್ಪರ್ಶಕಗಳಿಂದಾದ ಕ್ಷೇತ್ರರಚನೆಯಲ್ಲಿ ಕನಿಷ್ಠ ಒಂದು ಬಿಂದುವಿನಲ್ಲಾದರೂ ನಿವ್ವಳ ಕ್ಷೇತ್ರ ಶೂನ್ಯವಾಗಿರುತ್ತದೆ. ಏನಾದ್ರೂ ಅರ್ಥ ಆಯ್ತಾ? ಅಥವಾ ತಲೆಯ ಮೇಲಿಂದ ಹಾರಿಹೋಯ್ತಾ? ಪರವಾಗಿಲ್ಲ ಬಿಡಿ. ಗಣಿತದ ಭಾಷೆ ಗಣಿತಜ್ಞರಿಗಷ್ಟೇ ಇರಲಿ. ನಮಗೆ ‘ಕೂದಲಿನ ಚೆಂಡು’ ಮಾದರಿಯೇ ಇರಲಿ. 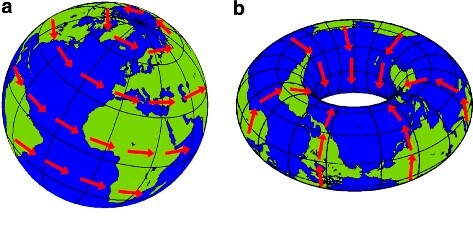ಅಷ್ಟಕ್ಕೂ ಈ ಪ್ರಮೇಯದ ಪ್ರಯೋಜನವಾದರೂ ಏನು? ಅದನ್ನು ತಿಳಿದುಕೊಳ್ಳಬೇಕಿದ್ದರೆ ಇವತ್ತಿನ ಶೀರ್ಷಿಕೆಯ ದ್ವಿತೀಯಾರ್ಧವನ್ನು ಇನ್ನೊಮ್ಮೆ ಗಮನಿಸೋಣ. ಬೀಸುವ ತಂಗಾಳಿಯ ವಿಷಯವೇನೆಂದು ತಿಳಿದುಕೊಳ್ಳೋಣ. ಭೂಮಿಯನ್ನು ಒಂದು ಚೆಂಡು ಎಂದು ಪರಿಗಣಿಸಿದರೆ ಅದರ ಸುತ್ತಲಿನ ವಾತಾವರಣವೇ ಕೂದಲುಗಳು. ಒಂದು ನಿರ್ದಿಷ್ಟ ದಿಕ್ಕಿನಲ್ಲಿ ಗಾಳಿ ಬೀಸುತ್ತಿದೆಯೆಂದರೆ ಭೂಮಿಯ ಕೂದಲುಗಳನ್ನು ಮಟ್ಟಸವಾಗಿ ಬಾಚಿದಂತೆ. ನಮ್ಮ ಪ್ರಮೇಯ ಏನು ಸಾಧಿಸುತ್ತದೆಯೆಂದರೆ ಭೂಮಂಡಲವಿಡೀ ಸದಾ ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಗಾಳಿ ಬೀಸಿ ಭೂಮಿಯನ್ನು ಆವರಿಸುವುದು ಸಾಧ್ಯವಿಲ್ಲ. ಎಲ್ಲೋ ಒಂದು ಕಡೆ ಗಾಳಿಯ ವೇಗ ಸೊನ್ನೆ ಇರುತ್ತದೆ. ಅಥವಾ, ಭೂಮಿಯ ಮೇಲ್ಮೈಗೆ ಲಂಬಕೋನದಲ್ಲಿ ಗಾಳಿ ಬೀಸುತ್ತದೆ. ಅದನ್ನೇ ನಾವು ಸುಂಟರಗಾಳಿ ಎನ್ನುತ್ತೇವೆ. ಅಂದರೆ, ವಾತಾವರಣದಲ್ಲಿ ಬೀಸುವ ಗಾಳಿಯನ್ನು ಭೂಮಿಯೆಂಬ ತಲೆಯ ಬಾಚಿದ ಕೂದಲು ಎಂದುಕೊಂಡರೆ ಅಲ್ಲಿಯೂ ನಮ್ಮ ತಲೆಯಂತೆಯ ಸುಳಿ, ಬೈತಲೆ, ಜುಟ್ಟು, ಕೆದರಿದ ಕೂದಲು ಎಲ್ಲ ಇರುತ್ತವೆ! ಹಾಗಾಗಿಯೇ ಪ್ರಪಂಚದಲ್ಲಿ ಇಷ್ಟೆಲ್ಲ ಪ್ರಾಕೃತಿಕ ಏರುಪೇರುಗಳು. ತಮಾಷೆಯಲ್ಲ, ಜಾಗತಿಕ ಹವಾಮಾನ ಅಧ್ಯಯನದಲ್ಲಿ ಈ ಪ್ರಮೇಯ ಅತ್ಯಂತ ಮಹತ್ವದ್ದಾಗುತ್ತದೆ. ಆದರೆ ಗೋಲಾಕಾರದ ವಸ್ತುಗಳಿಗೆ ಮಾತ್ರ ಇದು ಅನ್ವಯವೇ? ಹಾಗೇನಿಲ್ಲ. ನಮ್ಮ ತಲೆಯೇ ಪರಿಪೂರ್ಣ ಗೋಲ ಅಲ್ಲವಲ್ಲ? ಎಲ್ಲ ಚೆಂಡುಗಳೂ ಗೋಲಾಕಾರ ಅಂತೇನಿಲ್ಲ. ‘ರಗ್ಬಿ’ ಆಟದ ಚೆಂಡು ಮತ್ತು ಅಮೆರಿಕದ ಫುಟ್‌ಬಾಲ್ ಆಟದ ಚೆಂಡು ಗೋಲಾಕಾರವಲ್ಲ. ಮೊಟ್ಟೆಯಂತೆ ಉದ್ದುದ್ದವಾಗಿ ಇರುತ್ತವೆ. ಅವುಗಳ ಮೇಲೆ ಕೂದಲು ಇರುವುದಿಲ್ಲವಾದರೂ ಒಂದೊಮ್ಮೆ ಇದೆಯೆಂದು ಭಾವಿಸಿ ಬಾಚಿದರೆ ಪ್ರಮೇಯದಂತೆಯೇ ಆಗುತ್ತದೆ. ಚೆಂಡಿನೊಳಗಿನ ಗಾಳಿ ಖಾಲಿಯಾಗಿ ಚಪ್ಪಟೆಯಾದರೂ ಪ್ರಮೇಯದ ಬದ್ಧತೆಗೆ ಭಂಗವಾಗುವುದಿಲ್ಲ. ಒಂದುವೇಳೆ ಗೋಲ ಚಪ್ಪಟೆಯಾಗಿ ನಡುವೆ ತೂತಿದ್ದರೆ? ಆ ಆಕಾರವನ್ನು ಗಣಿತದಲ್ಲಿ torus ಎನ್ನುತ್ತಾರೆ. ತತ್‌ಕ್ಷಣಕ್ಕೆ ನೆನಪಾಗುವ ಉದಾಹರಣೆಗಳೆಂದರೆ ಉದ್ದಿನವಡೆ, ಕೋಡುಬಳೆ, ಡೋನಟ್, ಬೇಗಲ್, ಟೆನ್ನಿಕಾಯ್ಟ್ ರಿಂಗ್, ಗಾಳಿ ತುಂಬಿದ ಟೈರ್‌ಟ್ಯೂಬ್ ಇತ್ಯಾದಿ. ಟೋರಸ್ ಆಕಾರದ ವಸ್ತುವಿನ ಮೇಲೆ ಕೂದಲನ್ನು ಮಟ್ಟಸವಾಗಿ ಬಾಚುವುದು ಸಾಧ್ಯ! ನಡುವಿನ ತೂತಿನ ಸುತ್ತ ನೀಟಾಗಿ ಬಾಚಿದರಾಯ್ತು ಇಡೀ ವಸ್ತುವನ್ನು ಕೂದಲಿನಿಂದ ಮುಚ್ಚುವುದಕ್ಕಾಗುತ್ತದೆ. ಇದೇ ತತ್ತ್ವದಲ್ಲಿ ನಮ್ಮ ಭೂಮಿ ದುಂಡಗಿರದೆ ಟೋರಸ್ ಆಕಾರದಲ್ಲಿರುತ್ತಿದ್ದರೆ ಇಡೀ ಭೂಮಂಡಲದಲ್ಲಿ ಒಂದೇ ದಿಕ್ಕಿನಲ್ಲಿ ಗಾಳಿ ಬೀಸುವುದು ಸಾಧ್ಯವಾಗುತ್ತದೆ; ಹಾಗೆಯೇ ನಮ್ಮ ತಲೆಯೂ ನಡುವೆ ತೂತಿರುವ ಟೊಳ್ಳು ಬುರುಡೆ ಆಗಿರುತ್ತಿದ್ದರೆ ತಲೆಗೂದಲನ್ನು ಮಟ್ಟಸವಾಗಿ ಬಾಚಿ ತಲೆಯನ್ನು ಸಂಪೂರ್ಣ ಮುಚ್ಚುವುದು ಸಾಧ್ಯವಾಗುತ್ತದೆ! ಅಂದಹಾಗೆ Hairy Ball theorem ಎಂಬ ಇಂಗ್ಲಿಷ್ ಹೆಸರು ಏನಿದ್ರೂ ಕೊಂಚ ಕೆಳಮಟ್ಟದ್ದೇ ಆಗಿದೆ;-) ಅದರ ಬದಲು ‘ಕೇಶಕಂದುಕ ಪ್ರಮೇಯಮ್’ ಎಂದು ಸಭ್ಯ ಸುಸಂಸ್ಕೃತ ಹೆಸರಿಟ್ಟರೆ ಹೇಗೆ? * * * [ಈ ಲೇಖನವನ್ನು ನೀವು ವಿಜಯ ಕರ್ನಾಟಕ ಇ-ಪೇಪರ್‌ನಲ್ಲಿಯೂ ಓದಬಹುದು.] "Listen Now" ಮೇಲೆ ಕ್ಲಿಕ್ಕಿಸಿದರೆ ಕೇಳಿ ಆನಂದಿಸಬಹುದು!